Here is my GitHub page.

Matrix data arising in modern applications often requires joint modeling to handle observed and unobserved row-specific and column-specific factors. Generalized bilinear models (GBMs) are a flexible extension of generalized linear models (GLMs) to include latent factors as well as row covariates, column covariates, and interactions to analyze high-dimensional matrix data. BilinearModels is a Julia package for estimation and inference in negative binomial GBMs for large matrices of count data. For background, see the publication:

Inference in generalized bilinear models, J. W. Miller and S. L. Carter, 2020. (pdf) (arXiv)

Click here for more information and for downloading.

BayesianMixtures is a Julia package for nonparametric Bayesian mixture models and Bayesian clustering. The following model types are currently implemented:

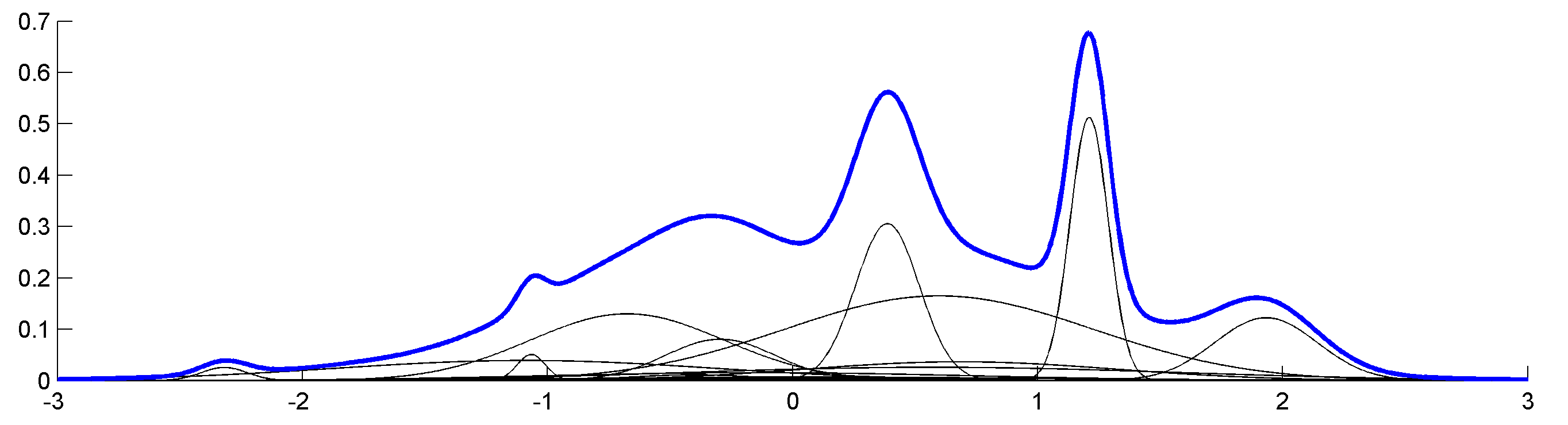
• mixture with a prior on the number of components, a.k.a., mixture of finite mixtures (MFM), and
• Dirichlet process mixture.

The following component distributions are currently implemented:

• univariate normal,
• multivariate normal with diagonal covariance matrix, and
• multivariate normal (with unconstrained covariance matrix).

For all models, inference is performed using the Jain-Neal split-merge samplers. For MFMs, this is done using the results from our article:

Mixture models with a prior on the number of components, J. W. Miller and M. T. Harrison, Journal of the American Statistical Association (JASA), Vol. 113, 2018, pp. 340-356. (pub) (pdf) (arXiv)

Click here for more information and for downloading.

Gshape.jl provides a fast and simple algorithm for approximating the full conditional distribution of the shape parameter of a gamma distribution, using a gamma distribution for the approximation. See the article for details:

Fast and accurate approximation of the full conditional for gamma shape parameters, J. W. Miller, 2018. (pdf)

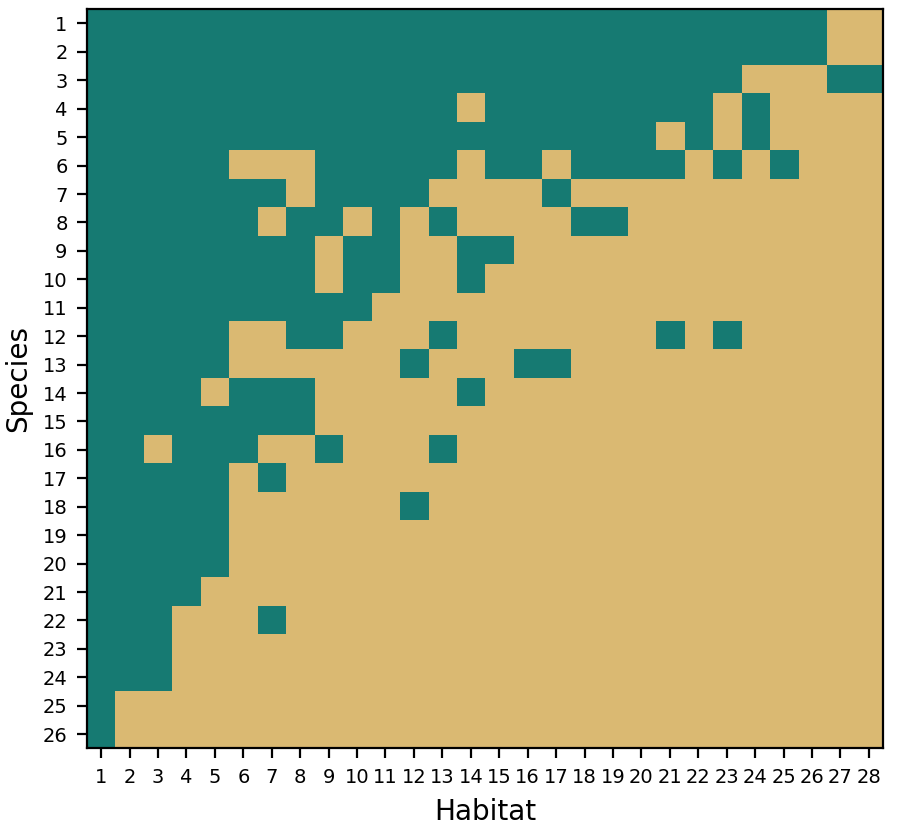EXACT is a software package for exact counting and exact sampling of binary or non-negative integer matrices with specified row and column sums. (Download version 0.3 here.) Note: This program is only applicable for matrices of moderate size — smaller than 40x40 or so — or very sparse larger matrices. The program can be very memory intensive, so if you give it a problem that is too difficult, it will probably allocate all of your available RAM and then get bogged down (so you might want to keep an eye on how much RAM it's using).

For larger matrices, we provide a sequential importance sampling algorithm that is very efficient and often is very close to exact. A Matlab implementation of this is available in the folder \examples\total variation distance of the EXACT package.

Features

• A fast C implementation
• Wrappers for Matlab, Python, and R
• Python implementation (binary matrices only)
• Example code and demonstrations for several applications

Applications

• Null model analysis of ecological matrices
• Conditional volume test for contingency tables with small margins
• Social network analysis (for small networks)
• Computing the Ehrhart polynomials
• Assessing the accuracy of approximate sampling methods for such matrices

References

Exact sampling and counting for fixed-margin matrices, J. W. Miller and M. T. Harrison, The Annals of Statistics, Vol. 41, No. 3, 2013, pp. 1569-1592. (pub) (pdf) (arXiv)

Importance sampling for weighted binary random matrices with specified margins, M. T. Harrison and J. W. Miller, (In preparation). (pdf) (arXiv)

 

© 2022 Jeffrey W. Miller